Average Example 1
Problem Find the average, and average
deviation
for the following data on the length of a pen, L. We have 5
measurements,
(12.2, 12.5, 11.9,12.3, 12.2) cm.
| Length (cm) |
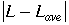 | | |
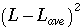 |
| 12.2 |
0.02 |
0.0004 |
| 12.5 |
0.28 |
0.0784 |
| 11.9 |
0.32 |
0.1024 |
| 12.3 |
0.08 |
0.0064 |
| 12.2 |
0.02 |
0.0004 |
| Sum 61.1 |
Sum 0.72 |
Sum 0.1880 |
| Average 61.1/5 = 12.22 |
Average 0.14 |
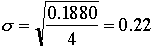 |
To get the average sum the values and divide by the number of measurements.
To get the average deviation,
- Find the deviations, the absolute values of the quantity (value minus the average), |L - Lave|
- Sum the absolute deviations,
- Get the average absolute deviation by dividing by the number of measurements
To get the standard deviation
- Find the deviations and square them
- Sum the squares
- Divide by (N-1), the number of measurements minus 1 (here it is 4)
- Take the square root.
The pen has a length of (12.22 +/- 0.14) cm or (12.2 +/- 0.1) cm [using average deviations] or
(12.22 +/- 0.22) cm or (12.2 +/- 0.2) cm [using standard deviations].
Return (or use Browser "back"
function)
Average Example 2
Problem: Find the average and the average deviation of the following measurements of a mass.
(4.32, 4.35, 4.31, 4.36, 4.37, 4.34) grams.
| Mass (grams) |
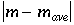 |
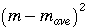 |
| 4.32 |
0.0217 |
0.000471 |
| 4.35 |
0.0083 |
0.000069 |
| 4.31 |
0.0317 |
0.001005 |
| 4.36 |
0.0183 |
0.000335 |
| 4.37 |
0.0283 |
0.000801 |
| 4.34 |
0.0017 |
0.000003 |
| Sum 26.05 |
0.1100 |
0.002684 |
| Average 4.3417 |
Average 0.022 |
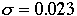 |
The same rules as Example 1 are applied. This time there are N = 6 measurements, so for the standard deviation we divide by (N-1) = 5.
The mass is (4.342 +/- 0.022) g or (4.34 +/- 0.02) g [using average deviations] or
(4.342 +/- 0.023) g or (4.34 +/- 0.02) g [using standard deviations].
Return (or use Browser "back" function)